ポケモンGOのレイドデイでいかに多くのジムを回るかについて考察した本を書いていました。過去形。
もともとはC98に向けて書いていたものですが、コロナ禍で中止になって執筆モチベが下がり、リモートレイドパスの実装によって執筆モチベがゼロになりました。
記憶から抹消するのももったいなかったので公開します。それではどうぞ。
はじめに
Pokémon GO(以下、ポケモンGO)はポケモンのスマホゲーである。ポケモンGOではたまに「レイドバトルデイ」と呼ばれる、レイドボスがある期間中(基本は3時間)大量に出現するイベントが開催されている。レイドバトルデイの日、ポケモントレーナーたちは色違いや高個体値のポケモンを求め、じゃぶじゃぶレイドパスに課金して3時間ぶっ続けでポケモンを捕まえるのだ。炎天下で6時間もぶっ通しでフリーザーを捕まえまくったときは本当に大変だった。
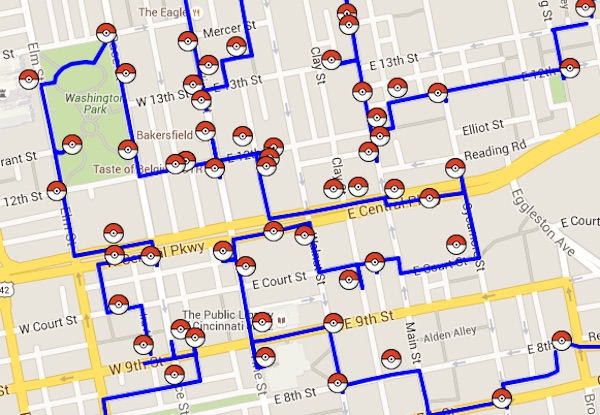
まあそんなことは置いておいて、ある日のこと。ポケモンGOを嗜む友人とLINEでやり取りしていたところ、レイドバトルデイで多くのジムを回れるルートを記した画像が

というメッセージとともに送られてきた。

しかしめんどくさい私は
本当にそれって最適なの?
もっと良いルートがあるんじゃない?
理論的に求められるんじゃない?
と思ってしまったのだった。そういう理屈っぽくて難しいことは他の人が研究してネットに結果を載せておいてくれればよかったのだが、残念なことにググっても良さげな情報は見つからなかったので自分で調べることにした、というのが本書の導入である。

分かる人いたら教えてくれると助かります。
既存の研究的なものの紹介
前節で「ググっても良さげな情報は見つからなかった」と書いたが、良いかどうかは置いておいてポケモンGOを論理的に効率化する情報自体はいくつか存在する。
カナダにあるウォータールー大学のWilliam Cookら は、巡回セールスマン問題の例としてアメリカのシンシナティ市にある551のジム・ポケストップを最短距離で巡回するルートを計算し、そのルートを公開している 。巡回セールスマン問題とは、ある地点を出発してから他のすべての地点(この場合はジムとポケストップ)を1度ずつ訪れてまた出発地点に戻ってくるような経路のうち最短のものを求める問題だ。
しかし実際のゲームで考えると、このようにすべてのポケストップを最短経路で回ることが最も効率が良いとは限らない。上の例でも、5分待てばポケストップを再び回せるわけだから、それ以上の時間をかけてさらに長距離を歩くことに直接的な優位性はない。5分程度 で周回できるような、ポケストップが密集したルートを探すほうが効果的だ。Mathematics Stack Exchangeでは「What is the optimal route for visiting Pokéstops in Pokémon Go?」という題でポケストップから延々と道具を入手するために5分で1周するルートを求める方法について議論されている 。5分で1周できる円をかいて、その内外50mのドーナツ状領域の中に含まれるポケストップの数を最大化するような位置を探せばいいんじゃない?というヒューリスティックな手法が提案されていた。みんな頭いい。
そして、レイドバトルデイで多くのレイドボスを倒す場合も同様に、すべてのジムを回る必要はない。それに加え、出発地に戻ってくるような環状の巡回路である必要もない。決められた時間(1時間や3時間)内にできるだけ多くのジムを回ってレイドボスを倒すことが求められる。
今回やることの紹介
レイドバトルデイで「一定の時間内になるべく多くのジムを巡るにはどうすればいいか」というような、何らかの条件のもとでできるだけ〇〇したいというテーマは、数学チックにいうと“最適化問題”と呼ばれる。最適化問題は「できるだけ〇〇したい」を表す“目的関数”と「何らかの条件」を表す“制約条件”から構成されている。例えばレイドバトルデーの制限時間内に訪れるジムの数を最大にする
最適化問題は、以下のように表される。
目的関数:訪れるジムの数を最大化する
制約条件:異なるn個のジムからいくつかを選んで順番に回るルートを設定する
というようになる。出発地へ戻ってこないというのが重要で、巡回セールスマン問題やその類題との大きな差である。
これでもいいのだが、本書ではちょっと変えて
目的関数:訪れるジムを回る距離を最小化する
制約条件:異なるn個のジムからm個を選んで順番に回るルートを設定する
という問題を解くことにした。なぜこう変えてしまったのかというと、「このほうが巡回セールスマン問題っぽいから解き方を流用できたらいいな」と考えてこの形式でコードを書き始めてしまったからである。ついでにこの問題をレイドめぐりトレーナー問題(Raiding Trainer Problem, RTP )と名付けた。あ、このRTPっていうオレオレ略称はこれからどんどん使ってくから覚えておいてね。
RTPのような、整数などの離散的な値から構成される最適化問題のことを特に“組合せ最適化”という。組合せ最適化の問題の一部は多項式時間で解けない(解くのに非常に時間がかかる)ことが知られていて、RTPも多分きっとそれに属している。単純に総当たりで解こうとすると、n個のジムのうちm個を訪れる場合の数はnPm⁄2=n!⁄2(n-m)!通り。128個のジムから45個を選んで訪れる場合だと約4.9×10^90通りにもなるのだ(Pythonで計算させたところ、488 6809 5254 5172 5756 7192 8567 1886 2717 7580 5553 2360 6473 2239 0590 7113 9721 6838 5154 2528 0000 0000 0000通りだった)。
もちろん人間も手をこまねいているわけではなく、工夫して総当たり回数を減らして最適解を得る方法や、最適解は得られなくとも「そこそこ最適っぽい解」が得られるようなヒューリスティックな方法が数多く開発されている。そのあたりの人類の叡智をほどほどに使って冒頭のレイドバトルデイのルートよりも良いルートを見つけたいと思う。
ということで「組合せ最適化でポケモンGO効率化」、スタートです。
準備
ジムの座標情報の取得
RTPを解くにあたって、まずはジムがどこにあるかという座標情報が必要だ。本書ではポケマピのマップ共有サービス「GO FRIEND」の座標情報を利用させてもらった。この座標情報は以下の手順によりChromeなどのブラウザ で簡単に取得できる。
まずGO FRIENDのWebサイト https://go-friend.com/map/ にアクセスする。調べたいのはジムのみなので、右上のトグルを
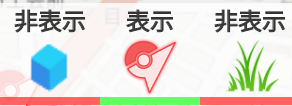
のようにしておく。そして、調べたい地域の地図を表示する。

F12キーで開発者ツールを起動してNetworkタブを開き、そして地図をわずかに動かすと「map_json.php」というセッションが記録されるはずだ。

この「map_json.php」のあたりを右クリックして「Copy」→「Copy response」と選択すればレスポンスの内容がクリップボードにコピーされる。そのままではとても読めたものではないが、適当に整形処理を行うと 次のようになる。

これの”pm_lat”と”pm_lng”がそれぞれ緯度、経度 にあたる。あとはこれをローカルに保存すればOK。
ジムの座標情報の処理
各ジムの緯度・経度がわかったので、次は各ジム間の距離(測地線長)を緯度・経度から求めてみる。地球を楕円体として考えて緯度・経度から測地線長を厳密に計算する式が国土地理院のサイトに掲載されている…が、正直なところ面倒なので本書では次に示すような荒い近似を用いた。
すべてのジムが北緯35°、東経135°に十分近い位置にあり、地球表面を平面とみなせると仮定する。そして、緯度・経度 [°] で表される2つのジムの座標 (ϕ1, λ1), (ϕ2, λ2) を、mの単位を持つ平面xy座標 (x1, y1), (x2, y2) に落とし込むことを考える。地球を半径 r の球として考えると、経線上での緯度差 Δϕ、北緯35°線上での経度差 Δλ をそれぞれ距離差 Δx、Δy に変換するには
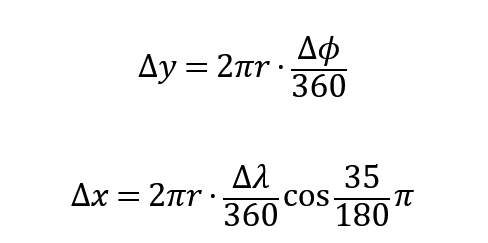
とすればいい。2つのジムの緯度・経度による座標 (ϕ1, λ1), (ϕ2, λ2) および変換したxy座標 (x1, y1), (x2, y2) を用いて変形すると、

となるような写像fが定義できる。
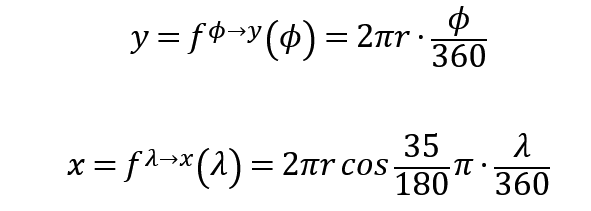
これらを用いることで、緯度・経度で表されるジムの座標をメートルの単位をもつ座標に変換できる。なお、本書では数字を扱いやすい大きさにするため、 ϕ, λ から35、135を引いて正規化した次の式を用いている。
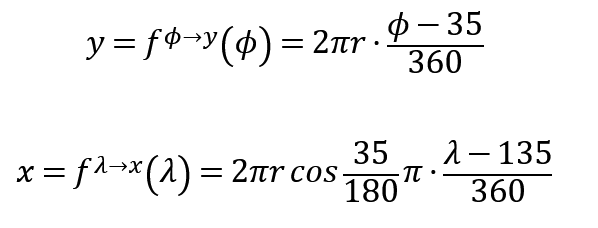
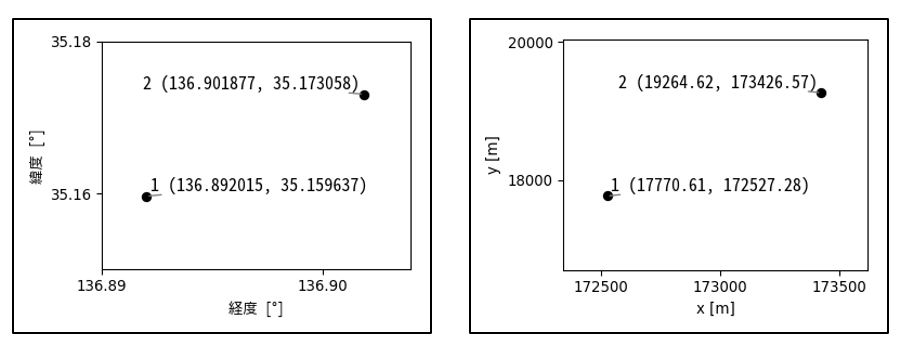
三平方の定理を適用し、変換した座標 (x1, y1), (x2, y2) を用いて2つのジム間の距離L12 [m]を近似的に求める。
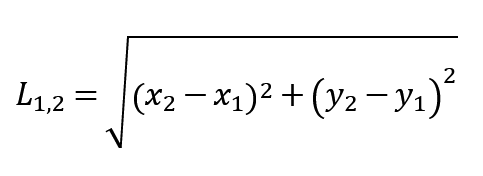
調査に使ったデータ
本書では、愛知県内でも特にポケモントレーナーが集まりやすいエリアである名古屋駅から久屋大通あたりに分布する128個のジムについて調査を行った。「はじめに」の節で示した45箇所のジムもここにすべて含まれている。

目的関数の設定
しばらく前に述べたとおり、RTPは次のような問題だ。
目的関数:訪れるジムを回る距離を最小化する
制約条件:異なるn個のジムからm個を選んで順番に回るルートを設定する
この目的関数Φをそのままシンプルに表記するなら、1番目と2番目のジム間の距離L_(1,2)からm-1番目とm番目のジム間の距離L_(m-1,m)までの和、すなわち
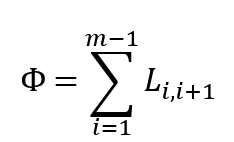
と表せる。しかし、実際のゲームでは
- ジムから50m以内ならレイドバトルに参加できる(ロビーに入ることができる)
- ジムから100m以内ならレイドバトルを始められる/ゲットチャレンジを行える
という仕様になっている。そのため、あるジムAでレイドバトルをして、次のジムB方向に100m進んだところでゲットチャレンジを行い、ジムBから50mの距離の時点で次のレイドバトルを行うことで、実質的に150m分の移動距離を節約することができる。

これを目的関数の計算に組み込んでみよう。ぎりぎりの位置でGPSがブレてゲットチャレンジから弾かれてもいけないので150m分きっちり節約できるわけではないが、それでも50m分くらいは実質移動距離を減らせそうだ。それを加味すると、RTPの目的関数は実質移動距離L ̃を用いて
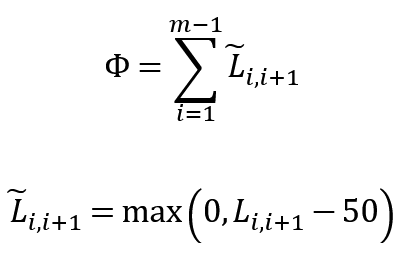
というふうに設定できる。
RTPを解いてみよう
さてさて、準備も整ったことだから早速RTPを解いてみよう。目標は単純だ。最初に出したレイドバトルデイのルート(以下、初期ルート)よりも移動距離の短い優れたルートを求めること。求めるツールとして本書ではPython 3.7を用いている。
まず初期ルートについて。初期ルートの目的関数値(L ̃を用いた実質移動距離)は5426.0 [m]、Lを用いた実際の移動距離は7539.7 [m]だ。このルートをグラフに表すと次のようになる。matplotlib+adjust_textで機械的にプロットしたので少し見にくいが、愛の形からスタートしてITO EN キングジョイ2階VDコーナーまで行くルートだ。

貪欲法で解いてみる
まずは単純なアルゴリズムの1つである貪欲法で解いてみよう。貪欲法はスタート地点のジムを決めたらそこから一番近いジムを順に選んでいくという方法だ。初期ルートに倣って「愛の形」をスタート地点にしてみた。
結果は次の図だ。金時計のあたりまでは調子がよかったが、そのあと西へ行って迷走する感じになってしまった。あ~あ。目的関数値は8211.6 [m]、Lを用いた実際の移動距離は10349.1 [m]。計算時間は0.1秒くらいで高速である。

ビームサーチで解いてみる
貪欲法ではあまり良い解は得られなかった。次はビームサーチで解いてみよう。ビームサーチでは複数の候補――2番目以降に近いジムを同時に検討していくことで局所解に陥ってしまう可能性を低くしている。局所解はその名の通り、局所的には良い解だが全体で見ると良くない解のことだ。3.1節の貪欲法ではとにかく一番距離が近いジムを選んでいったことで近くのジムが尽きてしまい、最終的に迷走する結果となってしまった。ビーム幅(保持する候補の数)をいくつか変えて検証してみた。
ビーム幅10000で計算した結果が次である。目的関数値は3676.7 [m]、Lを用いた実際の移動距離は5759.0 [m]。計算時間は265秒だった。

目的関数の変更
ここまで目的関数として次の式を用いてきた。
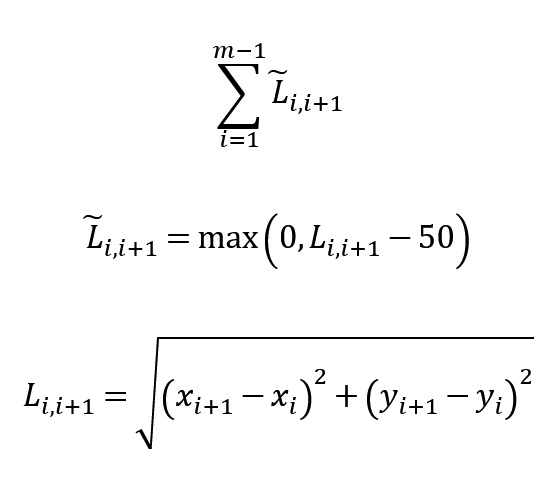
3番目の式はユークリッド距離と呼ばれる、要は普通の距離である。この根号を外すと――つまり
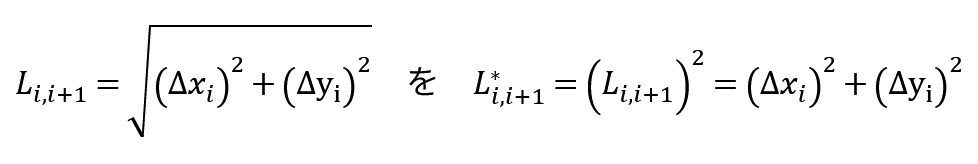
とユークリッド距離の2乗にして目的関数値を計算するとどうなるだろうか。例としてジム3つ分(順に1,2,3とする)の移動距離について考えてみる。それぞれの方法で目的関数値(簡単のためにL~ではなくLを用いる)を計算して次元を揃えてみると、

Φ(1→3)^*はΦ(1→3)と比較して2L_1,2 L_2,3という項が除算されていると見ることができる。相加・相乗平均の関係から
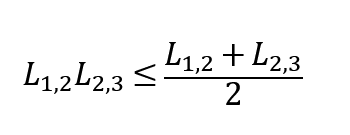
がいえ、L_1,2 L_2,3が最大となるのはL_1,2=L_2,3のときである。逆に言えば、L_1,2=L_2,3のときL_1,2 L_2,3が最大となり、目的関数Φ_(1→3)^*が最小となる。つまり、目的関数にユークリッド距離の2乗を用いることで、ルートに含まれる距離それぞれの値を近づけるような作用がはたらくと考えることができる。
経験上、次のジムまで長い距離を移動するこのような区間では、移動しながらゲットチャレンジで時間を潰そうとしてもすぐにポケモンが捕まってしまい、レイドバトルをしていない無駄な時間が生じやすい。目的関数にユークリッド距離の2乗を用いることでペナルティを与え、このような区間が生まれにくくなることが期待できる。
その他
整数計画問題として解いてみようとした
まずはイメージしやすい巡回セールスマン問題をMiller-Tucker-Zemlinの方法で定式化してみよう。n個のジムを巡回して元の地点に戻ってくるような問題は次のように表される。
目的関数
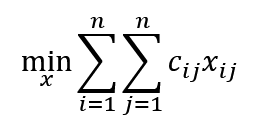
制約条件
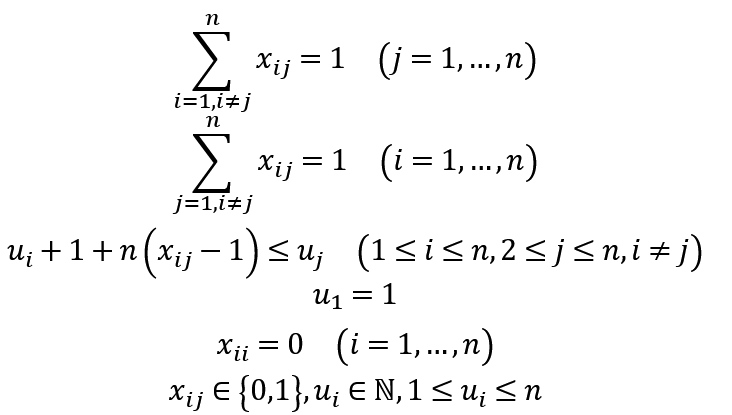
ここで、c_ijはジムiからジムjへ移動するコストを表し、cは移動コストを表す行列である。また x_ijは行列xのi行j列成分である。行列xはバイナリ変数を用いて移動経路を表していて、ジムiからジムjへ移動する場合はi行j列成分が1、しない場合は0となる。下の図は5つのジムを巡回するような例である。たとえば、x_3,5=1というのはジム3からジム5への移動を表現している。

ジムiからジムiへ向かうアークは存在しないから、xの対角成分x_iiは0だ。RTPではジムiからジムj、ジムjからジムiへの移動コストは変わらないから、cは対称行列になる。
1つ目と2つ目の制約条件は、あるジムへ入る矢印とそこから出る矢印がそれぞれ1本だけであることを示している。

3つ目と4つ目の制約条件は部分巡回路を除去するためにある。部分巡回路とは次の図のように一部のジムのみを巡回する経路のことだ。


さて、今度はRTPの定式化をする。全部でn個のジムのうちm個を巡回するようなRTPは次のようになる。
目的関数
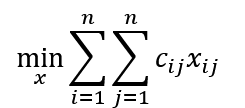
制約条件
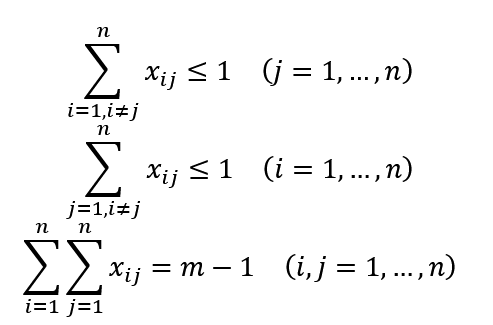
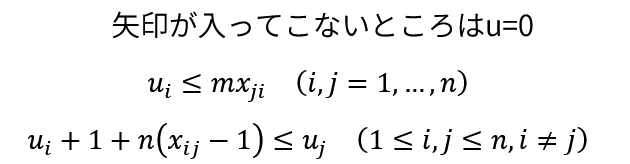
この(なんかいい感じの式)の部分に入る式を考えていきたい。
以上です
書きかけ感がすごいですね☆


コメント